| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 5 (Before Exercise 8.1) | Exercise 8.1 | Example 6 & 7 (Before Exercise 8.2) |
| Exercise 8.2 | ||
Chapter 8 Quadrilaterals
Welcome to the comprehensive solutions guide for Chapter 8, "Quadrilaterals," from the latest Class 9 NCERT mathematics textbook for the academic session 2024-25. This chapter significantly deepens the study of four-sided polygons, moving beyond basic definitions and classifications (covered in earlier classes) to rigorously prove and apply the numerous properties associated with these figures, particularly parallelograms and their special types. Mastering the concepts and proof techniques presented here is crucial for developing strong deductive reasoning skills in geometry. These solutions offer detailed, logical explanations and step-by-step proofs for all exercises, ensuring a thorough understanding of quadrilateral properties.
The chapter begins by reinforcing the fundamental Angle Sum Property of Quadrilaterals, confirming that the sum of the four interior angles always equals $360^\circ$. However, the primary focus quickly shifts to the important category of Parallelograms. The solutions provide meticulous, step-by-step deductive proofs for the essential properties that define a parallelogram:
- Theorem: Opposite sides of a parallelogram are equal.
- Theorem: Opposite angles of a parallelogram are equal.
- Theorem: The diagonals of a parallelogram bisect each other.
- Property: Adjacent angles of a parallelogram are supplementary.
Equally important are the conditions sufficient to prove that a quadrilateral is a parallelogram. The solutions demonstrate the proofs for these converse theorems, establishing that a quadrilateral is a parallelogram if:
- Both pairs of opposite sides are equal, OR
- Both pairs of opposite angles are equal, OR
- The diagonals bisect each other, OR
- One pair of opposite sides is both equal and parallel.
A highly significant theorem introduced and applied extensively in this chapter is the Mid-point Theorem. The solutions provide rigorous proofs for both the theorem and its converse:
- Mid-point Theorem: The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is half the length of the third side.
- Converse of the Mid-point Theorem: The line drawn through the mid-point of one side of a triangle, parallel to another side, bisects the third side.
Regarding the rationalized syllabus for 2024-25, Chapter 8, "Quadrilaterals," in the Class 9 NCERT textbook remains a core part of the curriculum. The fundamental concepts including the angle sum property, properties of parallelograms (and their converses), and the Mid-point Theorem (and its converse) are retained. The rationalization primarily involved streamlining the number and complexity of exercises and proofs, ensuring students master these essential theorems and their applications without being overwhelmed by exceptionally intricate deductive arguments. By engaging with these detailed solutions, students can learn to construct logical geometric proofs, master the properties of various quadrilaterals, and effectively apply the powerful Mid-point Theorem in problem-solving.
Example 1 to 5 (Before Exercise 8.1)
Example 1. Show that each angle of a rectangle is a right angle.
Answer:
Given:
A rectangle, say ABCD.
By definition, a rectangle is a quadrilateral with all its interior angles equal.
Let the measure of each interior angle be x.
So, $\angle$A = $\angle$B = $\angle$C = $\angle$D = x.
To Prove:
Each angle of the rectangle is a right angle, i.e., $\angle$A = $\angle$B = $\angle$C = $\angle$D = $90^\circ$.
Proof:
We know that the sum of the interior angles of any quadrilateral is $360^\circ$.
In rectangle ABCD, the sum of the interior angles is:
$\angle$A + $\angle$B + $\angle$C + $\angle$D = $360^\circ$
Since all angles are equal to x, we can substitute x into the equation:
x + x + x + x = $360^\circ$
Combine the terms on the left side:
4x = $360^\circ$
To find the value of x, divide both sides of the equation by 4:
x = $\frac{360^\circ}{4}$
x = $90^\circ$
Since each angle is equal to x, we have:
$\angle$A = $90^\circ$
$\angle$B = $90^\circ$
$\angle$C = $90^\circ$
$\angle$D = $90^\circ$
Therefore, each angle of a rectangle is a right angle.
Hence Proved.
Example 2. Show that the diagonals of a rhombus are perpendicular to each other.
Answer:
Given:
ABCD is a rhombus.
Its diagonals AC and BD intersect at point O.
To Prove:
The diagonals of the rhombus are perpendicular to each other.
i.e., AC $\perp$ BD, which means $\angle$ AOB = $90^\circ$ (or any angle formed by the intersection of diagonals).
Figure:
Draw a rhombus ABCD and its diagonals AC and BD intersecting at O.
Proof:
In a rhombus, all sides are equal. So, AB = BC = CD = DA.
Also, a rhombus is a special type of parallelogram, so its diagonals bisect each other.
Therefore, AO = CO and BO = DO.
Consider the triangles $\Delta$ AOB and $\Delta$ COB.
1. Side AB and side BC are equal.
AB = BC
(Sides of a rhombus are equal)
2. Side AO and side CO are equal.
AO = CO
(Diagonals of a parallelogram bisect each other, and a rhombus is a parallelogram)
3. Side BO is common to both triangles.
BO = BO
(Common side)
Therefore, by the SSS (Side-Side-Side) congruence criterion, $\Delta$ AOB is congruent to $\Delta$ COB.
$\Delta$ AOB $\cong$ $\Delta$ COB
... (i)
Since corresponding parts of congruent triangles are equal (CPCT), the corresponding angles $\angle$ AOB and $\angle$ COB are equal.
$\angle$ AOB = $\angle$ COB
(CPCT) ... (ii)
Also, $\angle$ AOB and $\angle$ COB form a linear pair on the straight line AC.
So, their sum is $180^\circ$ by the Linear Pair Axiom.
$\angle$ AOB + $\angle$ COB = $180^\circ$
(Linear Pair Axiom) ... (iii)
Substitute the value of $\angle$ COB from equation (ii) into equation (iii):
$\angle$ AOB + $\angle$ AOB = $180^\circ$
2$\angle$ AOB = $180^\circ$
Divide both sides by 2:
$\angle$ AOB = $\frac{180^\circ}{2}$
$\angle$ AOB = $90^\circ$
Since the angle formed by the intersection of the diagonals is $90^\circ$, the diagonal AC is perpendicular to the diagonal BD.
Hence, the diagonals of a rhombus are perpendicular to each other.
Hence Proved.
Example 3. ABC is an isosceles triangle in which AB = AC. AD bisects exterior angle PAC and CD || AB (see Fig. 8.8). Show that
(i) ∠DAC = ∠BCA and
(ii) ABCD is a parallelogram.
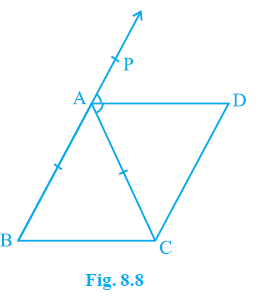
Answer:
Given:
ABC is an isosceles triangle with AB = AC.
AD bisects the exterior angle PAC.
CD || AB.
To Prove:
(i) $\angle$DAC = $\angle$BCA
(ii) ABCD is a parallelogram.
Proof:
(i) To show $\angle$DAC = $\angle$BCA:
In $\triangle$ABC, we are given AB = AC.
Therefore, the angles opposite to these equal sides are equal.
$\angle$ABC = $\angle$BCA
(Angles opposite to equal sides)
The exterior angle $\angle$PAC of $\triangle$ABC is equal to the sum of the two interior opposite angles.
$\angle$PAC = $\angle$ABC + $\angle$BCA
(Exterior angle property)
Since AD bisects $\angle$PAC,
$\angle$PAC = 2$\angle$DAC
... (i)
Substituting $\angle$ABC = $\angle$BCA into the exterior angle property:
$\angle$PAC = $\angle$BCA + $\angle$BCA
$\angle$PAC = 2$\angle$BCA
... (ii)
From (i) and (ii), we have:
2$\angle$DAC = 2$\angle$BCA
Dividing both sides by 2:
$\angle$DAC = $\angle$BCA
Thus, part (i) is proved.
Part (i) Proved.
(ii) To show ABCD is a parallelogram:
We are given that CD || AB.
From part (i), we have proved that $\angle$DAC = $\angle$BCA.
Consider lines AD and BC and transversal AC.
The angles $\angle$DAC and $\angle$BCA are alternate interior angles.
Since the alternate interior angles are equal, the lines AD and BC must be parallel.
AD || BC
(If alternate interior angles are equal, lines are parallel)
We have shown that both pairs of opposite sides are parallel:
CD || AB (Given)
AD || BC (Proved above)
A quadrilateral with both pairs of opposite sides parallel is a parallelogram.
Therefore, ABCD is a parallelogram.
Thus, part (ii) is proved.
Part (ii) Proved.
Example 4. Two parallel lines l and m are intersected by a transversal p (see Fig. 8.9). Show that the quadrilateral formed by the bisectors of interior angles is a rectangle.

Answer:
Given:
Two parallel lines $l$ and $m$ are intersected by a transversal $p$.
Let the transversal $p$ intersect the parallel line $l$ at point A and the parallel line $m$ at point C.
Let the bisectors of the interior angles form the quadrilateral ABCD, as shown in the figure.
To Prove:
The quadrilateral ABCD formed by the bisectors of the interior angles is a rectangle.
Proof:
We are given that line $l$ is parallel to line $m$ ($l$ || $m$), and $p$ is a transversal intersecting them at A and C respectively.
Consider the interior angles formed at A and C.
Let the bisector of $\angle$ PAC be AB and the bisector of $\angle$ ACR be DC, where $\angle$ PAC and $\angle$ ACR are alternate interior angles.
We know that when two parallel lines are intersected by a transversal, the alternate interior angles are equal.
$\angle$ PAC = $\angle$ ACR
(Alternate angles, as $l$ || $m$ and $p$ is a transversal)
Since AB is the bisector of $\angle$ PAC, $\angle$ BAC = $\frac{1}{2}\angle$ PAC.
Since DC is the bisector of $\angle$ ACR, $\angle$ ACD = $\frac{1}{2}\angle$ ACR.
Multiplying the equal angles by $\frac{1}{2}$, we get:
$\frac{1}{2} \angle$ PAC = $\frac{1}{2} \angle$ ACR
So, by substitution,
$\angle$ BAC = $\angle$ ACD
These angles, $\angle$ BAC and $\angle$ ACD, form a pair of alternate interior angles for the lines AB and DC with transversal AC. Since these alternate interior angles are equal, the lines AB and DC must be parallel.
AB || DC
Similarly, considering the other pair of interior angles on the transversal AC (e.g., $\angle$ SAC and $\angle$ ACB) and their bisectors AD and BC:
$\angle$ SAC = $\angle$ ACQ
(Alternate angles, as $l$ || $m$ and $p$ is a transversal)
Since AD is the bisector of $\angle$ SAC, $\angle$ CAD = $\frac{1}{2}\angle$ SAC.
Since BC is the bisector of $\angle$ ACB, $\angle$ BCA = $\frac{1}{2}\angle$ ACQ.
Multiplying the equal angles by $\frac{1}{2}$, we get:
$\frac{1}{2} \angle$ SAC = $\frac{1}{2} \angle$ ACQ
So, by substitution,
$\angle$ CAD = $\angle$ BCA
These angles, $\angle$ CAD and $\angle$ BCA, form a pair of alternate interior angles for the lines AD and BC with transversal AC. Since these alternate interior angles are equal, the lines AD and BC must be parallel.
AD || BC
Since both pairs of opposite sides are parallel (AB || DC and AD || BC), the quadrilateral ABCD is a parallelogram.
Now, consider the adjacent interior angles on the same side of the transversal $p$ on line $l$. These angles form a linear pair (sum is $180^\circ$).
$\angle$ PAC + $\angle$ CAS = $180^\circ$
(Linear pair axiom, or angles on a straight line)
AB is the bisector of $\angle$ PAC, and AD is the bisector of $\angle$ CAS. Multiply the equation by $\frac{1}{2}$:
$\frac{1}{2} \angle$ PAC + $\frac{1}{2} \angle$ CAS = $\frac{1}{2} \times 180^\circ$
$\angle$ BAC + $\angle$ CAD = $90^\circ$
The angle $\angle$ BAD is the sum of the adjacent angles $\angle$ BAC and $\angle$ CAD.
$\angle$ BAD = $\angle$ BAC + $\angle$ CAD
Substitute the sum $\angle$ BAC + $\angle$ CAD = $90^\circ$:
$\angle$ BAD = $90^\circ$
So, ABCD is a parallelogram in which one angle ($\angle$ BAD) is $90^\circ$.
A parallelogram with one right angle is a rectangle.
Therefore, the quadrilateral formed by the bisectors of interior angles is a rectangle.
Hence Proved.
Example 5. Show that the bisectors of angles of a parallelogram form a rectangle.
Answer:
Given:
ABCD is a parallelogram.
The angle bisectors of $\angle$A, $\angle$B, $\angle$C, and $\angle$D intersect to form a quadrilateral EFGH inside the parallelogram.
To Prove:
The quadrilateral EFGH formed by the bisectors of the angles of parallelogram ABCD is a rectangle.
Figure:
Draw a parallelogram ABCD. Draw the bisectors of each interior angle. These bisectors intersect at four points, forming an inner quadrilateral EFGH.
Proof:
In a parallelogram, adjacent angles are supplementary, meaning their sum is $180^\circ$.
Consider the adjacent angles $\angle$ A and $\angle$ D of parallelogram ABCD.
$\angle$ A + $\angle$ D = $180^\circ$
(Adjacent angles of a parallelogram)
The angle bisector of $\angle$ A is AE, and the angle bisector of $\angle$ D is DE. These bisectors intersect at point E, which is a vertex of the quadrilateral EFGH.
In $\Delta$ ADE, the angles are $\angle$ DAE, $\angle$ ADE, and $\angle$ AED.
Since AE bisects $\angle$ A, $\angle$ DAE = $\frac{1}{2}\angle$ A.
Since DE bisects $\angle$ D, $\angle$ ADE = $\frac{1}{2}\angle$ D.
By the Angle Sum Property of a triangle, the sum of interior angles in $\Delta$ ADE is $180^\circ$.
$\angle$ AED + $\angle$ DAE + $\angle$ ADE = $180^\circ$
(Sum of angles in a triangle)
Substitute the values of $\angle$ DAE and $\angle$ ADE:
$\angle$ AED + $\frac{1}{2}\angle$ A + $\frac{1}{2}\angle$ D = $180^\circ$
$\angle$ AED + $\frac{1}{2}(\angle$ A + $\angle$ D) = $180^\circ$
We know that $\angle$ A + $\angle$ D = $180^\circ$. Substitute this into the equation:
$\angle$ AED + $\frac{1}{2}(180^\circ)$ = $180^\circ$
$\angle$ AED + $90^\circ$ = $180^\circ$
Subtract $90^\circ$ from both sides:
$\angle$ AED = $180^\circ - 90^\circ$
$\angle$ AED = $90^\circ$
... (i)
The angle $\angle$ AED is the interior angle at vertex E of the quadrilateral EFGH (depending on labeling, it could also be $\angle$ HEF if the vertices are labeled differently). So, one angle of the quadrilateral is $90^\circ$.
Consider the adjacent angles $\angle$ A and $\angle$ B of parallelogram ABCD.
$\angle$ A + $\angle$ B = $180^\circ$
(Adjacent angles of a parallelogram)
The angle bisector of $\angle$ A is AF, and the angle bisector of $\angle$ B is BF. These bisectors intersect at point F, a vertex of EFGH, forming $\Delta$ ABF.
In $\Delta$ ABF, $\angle$ FAB = $\frac{1}{2}\angle$ A and $\angle$ FBA = $\frac{1}{2}\angle$ B.
Using the Angle Sum Property in $\Delta$ ABF:
$\angle$ AFB + $\angle$ FAB + $\angle$ FBA = $180^\circ$
Substitute the values:
$\angle$ AFB + $\frac{1}{2}\angle$ A + $\frac{1}{2}\angle$ B = $180^\circ$
$\angle$ AFB + $\frac{1}{2}(\angle$ A + $\angle$ B) = $180^\circ$
$\angle$ AFB + $\frac{1}{2}(180^\circ)$ = $180^\circ$
$\angle$ AFB + $90^\circ$ = $180^\circ$
$\angle$ AFB = $90^\circ$
... (ii)
The angle $\angle$ AFB is vertically opposite to the interior angle $\angle$ EFG of the quadrilateral EFGH.
$\angle$ EFG = $\angle$ AFB = $90^\circ$
(Vertically opposite angles)
Similarly, by considering $\Delta$ BCG (formed by bisectors of $\angle$ B and $\angle$ C) and $\Delta$ CDH (formed by bisectors of $\angle$ C and $\angle$ D), we can prove that their angles at the intersection points are $90^\circ$.
In $\Delta$ BCG, $\angle$ B + $\angle$ C = $180^\circ$. Bisectors intersect at G, so $\angle$ BGC = $180^\circ - (\frac{1}{2}\angle B + \frac{1}{2}\angle C) = 180^\circ - \frac{1}{2}(180^\circ) = 180^\circ - 90^\circ = 90^\circ$.
$\angle$ BGC = $90^\circ$
... (iii)
$\angle$ BGC is vertically opposite to the interior angle $\angle$ FGH of EFGH.
$\angle$ FGH = $90^\circ$
(Vertically opposite angles)
In $\Delta$ CDH, $\angle$ C + $\angle$ D = $180^\circ$. Bisectors intersect at H, so $\angle$ CHD = $180^\circ - (\frac{1}{2}\angle C + \frac{1}{2}\angle D) = 180^\circ - \frac{1}{2}(180^\circ) = 180^\circ - 90^\circ = 90^\circ$.
$\angle$ CHD = $90^\circ$
... (iv)
$\angle$ CHD is vertically opposite to the interior angle $\angle$ GHE of EFGH.
$\angle$ GHE = $90^\circ$
(Vertically opposite angles)
From equations (i), (ii), and the derivations from (iii) and (iv), we have shown that all four interior angles of the quadrilateral EFGH are $90^\circ$:
$\angle$ HEF = $90^\circ$
$\angle$ EFG = $90^\circ$
$\angle$ FGH = $90^\circ$
$\angle$ GHE = $90^\circ$
A quadrilateral with all four interior angles equal to $90^\circ$ is a rectangle.
Therefore, the bisectors of the angles of a parallelogram form a rectangle.
Hence Proved.
Exercise 8.1
Question 1. If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Answer:
Given:
ABCD is a parallelogram.
The diagonals AC and BD are equal, i.e., AC = BD.
To Prove:
Parallelogram ABCD is a rectangle.
Figure:
Draw a parallelogram ABCD and its diagonals AC and BD.
Proof:
Consider the triangles $\Delta$ ABC and $\Delta$ DCB.
We can show that these two triangles are congruent using the SSS (Side-Side-Side) congruence rule.
1. Side AB and side DC are equal.
AB = DC
(Opposite sides of a parallelogram are equal)
2. Side BC is common to both triangles.
BC = CB
(Common side)
3. The diagonals AC and BD are equal.
AC = BD
(Given)
Therefore, by the SSS congruence rule, $\Delta$ ABC is congruent to $\Delta$ DCB.
$\Delta$ ABC $\cong$ $\Delta$ DCB
... (i)
By CPCT (Corresponding Parts of Congruent Triangles), the corresponding angles of congruent triangles are equal.
The angle $\angle$ ABC in $\Delta$ ABC corresponds to the angle $\angle$ DCB in $\Delta$ DCB.
$\angle$ ABC = $\angle$ DCB
(CPCT) ... (ii)
Now, since ABCD is a parallelogram, the adjacent angles are supplementary. This means their sum is $180^\circ$.
So, the sum of adjacent angles $\angle$ ABC and $\angle$ DCB is $180^\circ$ (they are interior angles on the same side of transversal BC between parallel lines AB and DC).
$\angle$ ABC + $\angle$ DCB = $180^\circ$
(Consecutive Interior Angles are supplementary) ... (iii)
Substitute $\angle$ DCB = $\angle$ ABC (from equation (ii)) into equation (iii):
$\angle$ ABC + $\angle$ ABC = $180^\circ$
2$\angle$ ABC = $180^\circ$
Divide both sides by 2:
$\angle$ ABC = $\frac{180^\circ}{2}$
$\angle$ ABC = $90^\circ$
Since ABCD is a parallelogram and one of its interior angles ($\angle$ ABC) is $90^\circ$, it must be a rectangle.
A parallelogram with one right angle is a rectangle.
Hence, if the diagonals of a parallelogram are equal, then it is a rectangle.
Hence Proved.
Question 2. Show that the diagonals of a square are equal and bisect each other at right angles.
Answer:
Given:
ABCD is a square.
To Prove:
(i) Diagonals AC and BD are equal (AC = BD).
(ii) Diagonals AC and BD bisect each other (AO = OC and BO = OD, where O is the intersection point).
(iii) Diagonals AC and BD bisect each other at right angles ($\angle$ AOB = $\angle$ BOC = $\angle$ COD = $\angle$ DOA = $90^\circ$).
Figure:
Draw a square ABCD and its diagonals AC and BD intersecting at point O.
Proof:
A square is a special type of quadrilateral with the following properties:
1. All sides are equal (AB = BC = CD = DA).
2. All interior angles are right angles ($\angle$A = $\angle$B = $\angle$C = $\angle$D = $90^\circ$).
3. A square is also a parallelogram.
Part (i): Diagonals are equal.
Consider the triangles $\Delta$ ABC and $\Delta$ DCB.
1. Side AB and side DC are equal.
AB = DC
(Sides of a square are equal)
2. The angles $\angle$ ABC and $\angle$ DCB are right angles.
$\angle$ ABC = $\angle$ DCB = $90^\circ$
(Angles of a square are $90^\circ$)
3. Side BC is common to both triangles.
BC = CB
(Common side)
Therefore, by the SAS (Side-Angle-Side) congruence rule, $\Delta$ ABC is congruent to $\Delta$ DCB.
$\Delta$ ABC $\cong$ $\Delta$ DCB
... (i)
By CPCT (Corresponding Parts of Congruent Triangles), the corresponding parts are equal.
The diagonal AC in $\Delta$ ABC corresponds to the diagonal DB (or BD) in $\Delta$ DCB.
AC = BD
(CPCT)
Thus, the diagonals of a square are equal.
Part (ii): Diagonals bisect each other.
A square is a parallelogram.
One of the properties of a parallelogram is that its diagonals bisect each other.
Since ABCD is a parallelogram, its diagonals AC and BD bisect each other at their point of intersection O.
AO = OC
(Diagonals of a parallelogram bisect each other)
BO = OD
(Diagonals of a parallelogram bisect each other)
Part (iii): Diagonals bisect each other at right angles.
Consider the triangles $\Delta$ AOB and $\Delta$ COB.
1. Side AO and side CO are equal.
AO = CO
(Diagonals bisect each other - Proven in Part (ii))
2. Side OB is common to both triangles.
OB = OB
(Common side)
3. Side AB and side CB are equal.
AB = CB
(Sides of a square are equal)
Therefore, by the SSS (Side-Side-Side) congruence rule, $\Delta$ AOB is congruent to $\Delta$ COB.
$\Delta$ AOB $\cong$ $\Delta$ COB
... (ii)
By CPCT, the corresponding angles are equal.
$\angle$ AOB = $\angle$ COB
(CPCT) ... (iii)
Now, $\angle$ AOB and $\angle$ COB form a linear pair on the straight line AC. The sum of angles in a linear pair is $180^\circ$ by the Linear Pair Axiom.
$\angle$ AOB + $\angle$ COB = $180^\circ$
(Linear Pair Axiom) ... (iv)
Substitute $\angle$ COB = $\angle$ AOB (from equation (iii)) into equation (iv):
$\angle$ AOB + $\angle$ AOB = $180^\circ$
2$\angle$ AOB = $180^\circ$
Divide both sides by 2:
$\angle$ AOB = $\frac{180^\circ}{2}$
$\angle$ AOB = $90^\circ$
Since $\angle$ AOB = $90^\circ$, the diagonals are perpendicular at their intersection.
The angles around point O form vertically opposite pairs. Since $\angle$ AOB = $90^\circ$, its vertically opposite angle $\angle$ COD is also $90^\circ$.
$\angle$ COD = $\angle$ AOB = $90^\circ$
(Vertically Opposite Angles)
Similarly, $\angle$ COB = $90^\circ$ (from equation (iii)), so its vertically opposite angle $\angle$ DOA is also $90^\circ$.
$\angle$ DOA = $\angle$ COB = $90^\circ$
(Vertically Opposite Angles)
Thus, $\angle$ AOB = $\angle$ BOC = $\angle$ COD = $\angle$ DOA = $90^\circ$.
Hence, the diagonals of a square bisect each other at right angles.
Combining all parts (i), (ii), and (iii), we have shown that the diagonals of a square are equal and bisect each other at right angles.
Hence Proved.
Question 3. Diagonal AC of a parallelogram ABCD bisects ∠A (see Fig. 8.11). Show that
(i) it bisects ∠C also,
(ii) ABCD is a rhombus.
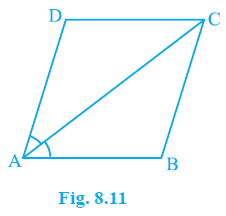
Answer:
Given:
ABCD is a parallelogram. The diagonal AC bisects $\angle A$, which means $\angle DAC = \angle BAC$.
To Prove:
(i) AC bisects $\angle C$, i.e., $\angle DCA = \angle BCA$.
(ii) ABCD is a rhombus (i.e., all sides are equal: AB = BC = CD = DA).
Proof:
Part (i): AC bisects $\angle C$.
Since ABCD is a parallelogram, we know that AB is parallel to DC and BC is parallel to AD.
Consider AB || DC and AC is a transversal.
The alternate interior angles are equal.
$\angle BAC = \angle DCA$
Consider BC || AD and AC is a transversal.
The alternate interior angles are equal.
$\angle BCA = \angle DAC$
We are given that AC bisects $\angle A$.
$\angle DAC = \angle BAC$
(Given)
From $\angle BAC = \angle DCA$, $\angle BCA = \angle DAC$, and $\angle DAC = \angle BAC$, we can conclude:
$\angle DCA = \angle BAC$ and $\angle BCA = \angle BAC$ (since $\angle DAC = \angle BAC$).
Therefore, $\angle DCA = \angle BCA$.
This shows that the diagonal AC bisects $\angle C$.
Part (ii): ABCD is a rhombus.
From Part (i), we have shown that $\angle BCA = \angle BAC$.
Consider $\triangle ABC$. In $\triangle ABC$, if $\angle BCA = \angle BAC$, then the sides opposite to these angles are equal.
The side opposite to $\angle BCA$ is AB.
The side opposite to $\angle BAC$ is BC.
So, AB = BC.
Since ABCD is a parallelogram, we know that opposite sides are equal: AB = CD and BC = AD.
We have proven that AB = BC.
Combining these equalities:
AB = BC
AB = CD (opposite to AB)
BC = AD (opposite to BC)
Therefore, AB = BC = CD = AD.
A parallelogram with all four sides equal is a rhombus.
Hence, ABCD is a rhombus.
Question 4. ABCD is a rectangle in which diagonal AC bisects ∠ A as well as ∠ C. Show that:
(i) ABCD is a square
(ii) diagonal BD bisects ∠ B as well as ∠ D.
Answer:
Given:
ABCD is a rectangle.
Diagonal AC bisects $\angle$ A as well as $\angle$ C.
This means $\angle$ DAC = $\angle$ BAC and $\angle$ BCA = $\angle$ DCA.
To Prove:
(i) ABCD is a square.
(ii) Diagonal BD bisects $\angle$ B as well as $\angle$ D.
Figure:
Draw a rectangle ABCD with diagonal AC drawn. Indicate that AC bisects angles A and C.
Proof:
Part (i): ABCD is a square.
Since ABCD is a rectangle, it is a parallelogram and all its interior angles are $90^\circ$.
$\angle$ A = $\angle$ B = $\angle$ C = $\angle$ D = $90^\circ$
(Angles of a rectangle)
We are given that diagonal AC bisects $\angle$ A.
$\angle$ BAC = $\angle$ DAC = $\frac{1}{2}\angle$ A
(Given AC bisects $\angle$ A)
Substituting $\angle$ A = $90^\circ$:
$\angle$ BAC = $\angle$ DAC = $\frac{1}{2}(90^\circ) = 45^\circ$
... (1)
We are also given that diagonal AC bisects $\angle$ C.
$\angle$ BCA = $\angle$ DCA = $\frac{1}{2}\angle$ C
(Given AC bisects $\angle$ C)
Substituting $\angle$ C = $90^\circ$:
$\angle$ BCA = $\angle$ DCA = $\frac{1}{2}(90^\circ) = 45^\circ$
... (2)
Consider $\Delta$ ABC.
From equation (1), $\angle$ BAC = $45^\circ$.
From equation (2), $\angle$ BCA = $45^\circ$.
Since $\angle$ BAC = $\angle$ BCA (both are $45^\circ$), $\Delta$ ABC is an isosceles triangle with the sides opposite to these angles being equal.
BC = AB
(Sides opposite equal angles in $\Delta$ ABC)
A rectangle is a parallelogram with all angles equal to $90^\circ$. We have shown that the adjacent sides AB and BC are equal.
A rectangle with a pair of equal adjacent sides is a square.
Therefore, ABCD is a square.
Part (ii): Diagonal BD bisects $\angle$ B as well as $\angle$ D.
Since ABCD is a square (proven in Part (i)), all its sides are equal.
AB = BC = CD = DA
(Sides of a square)
Consider $\Delta$ ABD.
AB = AD
(Sides of a square)
Since AB = AD, $\Delta$ ABD is an isosceles triangle. The angles opposite the equal sides are equal.
$\angle$ ABD = $\angle$ ADB
(Angles opposite equal sides)
In a square, $\angle$ A = $90^\circ$. By the Angle Sum Property in $\Delta$ ABD:
$\angle$ ABD + $\angle$ ADB + $\angle$ A = $180^\circ$
(Angle Sum Property)
Substitute $\angle$ ADB = $\angle$ ABD and $\angle$ A = $90^\circ$:
$\angle$ ABD + $\angle$ ABD + $90^\circ = 180^\circ$
2$\angle$ ABD = $180^\circ - 90^\circ$
2$\angle$ ABD = $90^\circ$
Divide by 2:
$\angle$ ABD = $45^\circ$
... (3)
Since $\angle$ ABD = $\angle$ ADB,
$\angle$ ADB = $45^\circ$
... (4)
Now, consider $\angle$ B of the square, which is $90^\circ$. $\angle$ B is composed of $\angle$ ABD and $\angle$ CBD.
$\angle$ B = $\angle$ ABD + $\angle$ CBD
Substitute $\angle$ B = $90^\circ$ and $\angle$ ABD = $45^\circ$ (from equation (3)):
90$^\circ$ = 45$^\circ$ + $\angle$ CBD
Subtract $45^\circ$ from both sides:
$\angle$ CBD = 90$^\circ$ - 45$^\circ$
$\angle$ CBD = $45^\circ$
Since $\angle$ ABD = $45^\circ$ and $\angle$ CBD = $45^\circ$, we have $\angle$ ABD = $\angle$ CBD. This shows that diagonal BD bisects $\angle$ B.
Now, consider $\angle$ D of the square, which is $90^\circ$. $\angle$ D is composed of $\angle$ ADB and $\angle$ CDB.
$\angle$ D = $\angle$ ADB + $\angle$ CDB
Substitute $\angle$ D = $90^\circ$ and $\angle$ ADB = $45^\circ$ (from equation (4)):
90$^\circ$ = 45$^\circ$ + $\angle$ CDB
Subtract $45^\circ$ from both sides:
$\angle$ CDB = 90$^\circ$ - 45$^\circ$
$\angle$ CDB = $45^\circ$
Since $\angle$ ADB = $45^\circ$ and $\angle$ CDB = $45^\circ$, we have $\angle$ ADB = $\angle$ CDB. This shows that diagonal BD bisects $\angle$ D.
Therefore, diagonal BD bisects $\angle$ B as well as $\angle$ D.
Hence Proved.
Question 5. In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig. 8.12). Show that:
(i) ∆ APD ≅ ∆ CQB
(ii) AP = CQ
(iii) ∆ AQB ≅ ∆ CPD
(iv) AQ = CP
(v) APCQ is a parallelogram
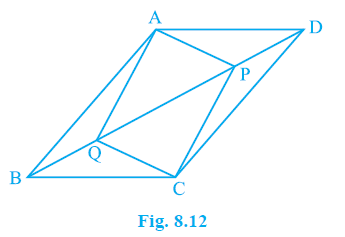
Answer:
Given:
ABCD is a parallelogram. Points P and Q are on the diagonal BD such that DP = BQ.
To Prove:
(i) $\triangle APD \cong \triangle CQB$
(ii) AP = CQ
(iii) $\triangle AQB \cong \triangle CPD$
(iv) AQ = CP
(v) APCQ is a parallelogram.
Proof:
Part (i): $\triangle APD \cong \triangle CQB$
Consider $\triangle APD$ and $\triangle CQB$.
AD = CB
(Opposite sides of a parallelogram are equal)
DP = BQ
(Given)
Since AD is parallel to BC and BD is a transversal, the alternate interior angles are equal.
$\angle ADB = \angle CBD$
(Alternate interior angles, AD || BC)
In terms of the points P and Q on BD, this is the same as:
$\angle ADP = \angle CBQ$
Therefore, by SAS congruence rule,
$\triangle APD \cong \triangle CQB$
Part (ii): AP = CQ
Since $\triangle APD \cong \triangle CQB$ (Proven in Part (i)), the corresponding parts are equal by CPCT (Corresponding Parts of Congruent Triangles are Congruent).
AP = CQ
Part (iii): $\triangle AQB \cong \triangle CPD$
Consider $\triangle AQB$ and $\triangle CPD$.
AB = CD
(Opposite sides of a parallelogram are equal)
BQ = DP
(Given)
Since AB is parallel to DC and BD is a transversal, the alternate interior angles are equal.
$\angle ABD = \angle CDB$
(Alternate interior angles, AB || DC)
In terms of the points Q and P on BD, this is the same as:
$\angle ABQ = \angle CDP$
Therefore, by SAS congruence rule,
$\triangle AQB \cong \triangle CPD$
Part (iv): AQ = CP
Since $\triangle AQB \cong \triangle CPD$ (Proven in Part (iii)), the corresponding parts are equal by CPCT.
AQ = CP
Part (v): APCQ is a parallelogram
From Part (ii), we have AP = CQ.
From Part (iv), we have AQ = CP.
A quadrilateral whose opposite sides are equal is a parallelogram.
In quadrilateral APCQ, we have shown that the pair of opposite sides (AP and CQ) are equal, and the other pair of opposite sides (AQ and CP) are also equal.
Therefore, APCQ is a parallelogram.
Question 6. ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (see Fig. 8.13). Show that
(i) ∆ APB ≅ ∆ CQD
(ii) AP = CQ
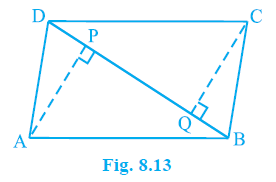
Answer:
Given:
ABCD is a parallelogram. AP $\perp$ BD and CQ $\perp$ BD, where P and Q are points on the diagonal BD.
To Prove:
(i) $\triangle APB \cong \triangle CQD$
(ii) AP = CQ
Proof:
Part (i): $\triangle APB \cong \triangle CQD$
Consider $\triangle APB$ and $\triangle CQD$.
We are given that AP is perpendicular to BD and CQ is perpendicular to BD.
$\angle APB = 90^\circ$
(Given AP $\perp$ BD)
$\angle CQD = 90^\circ$
(Given CQ $\perp$ BD)
Therefore, $\angle APB = \angle CQD$ (both are $90^\circ$).
Since ABCD is a parallelogram, its opposite sides are equal.
AB = CD
(Opposite sides of parallelogram ABCD)
Also, since ABCD is a parallelogram, AB is parallel to DC. BD is a transversal intersecting parallel lines AB and DC.
Therefore, the alternate interior angles are equal.
$\angle ABD = \angle CDB$
(Alternate interior angles, AB || DC)
In terms of the vertices of the triangles, this is the same as:
$\angle ABP = \angle CDQ$
Now, consider $\triangle APB$ and $\triangle CQD$ again:
$\angle ABP = \angle CDQ$
(Proven above)
$\angle APB = \angle CQD$
(Both $90^\circ$)
AB = CD
(Opposite sides of parallelogram)
Therefore, by AAS (Angle-Angle-Side) congruence rule,
$\triangle APB \cong \triangle CQD$
Part (ii): AP = CQ
Since $\triangle APB \cong \triangle CQD$ (Proven in Part (i)), the corresponding parts of the congruent triangles are equal by CPCT (Corresponding Parts of Congruent Triangles are Congruent).
AP = CQ
Hence, the perpendiculars from vertices A and C on diagonal BD are equal.
Question 7. ABCD is a trapezium in which AB || CD and AD = BC (see Fig. 8.14). Show that
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ∆ ABC ≅ ∆ BAD
(iv) diagonal AC = diagonal BD
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]
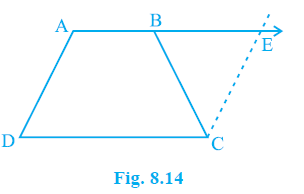
Answer:
Given:
ABCD is a trapezium with AB || CD and AD = BC.
To Prove:
(i) $\angle A = \angle B$
(ii) $\angle C = \angle D$
(iii) $\triangle ABC \cong \triangle BAD$
(iv) Diagonal AC = Diagonal BD
Proof:
Since AB || CD (given) and E is on the extension of AB, AE || CD.
Also, AD || CE (by construction).
Therefore, the quadrilateral ADCE is a parallelogram (since both pairs of opposite sides are parallel).
In a parallelogram, opposite sides are equal.
AD = CE
We are given that AD = BC.
AD = BC
(Given)
From the above two equations, we get:
BC = CE
Now consider $\triangle BCE$. Since BC = CE, $\triangle BCE$ is an isosceles triangle.
In an isosceles triangle, angles opposite the equal sides are equal.
So, $\angle CBE = \angle CEB$
On the straight line AE, $\angle ABC$ and $\angle CBE$ form a linear pair.
$\angle ABC + \angle CBE = 180^\circ$
$\angle ABC + \angle CBE = 180^\circ$
(Linear pair)
Since AD || CE and AE is a transversal, the consecutive interior angles are supplementary.
$\angle DAB + \angle AEC = 180^\circ$
Note that $\angle AEC$ is the same as $\angle CEB$.
So, $\angle DAB + \angle CEB = 180^\circ$
From $\angle CBE = \angle CEB$, we can substitute $\angle CBE$ for $\angle CEB$ in the above equation:
$\angle DAB + \angle CBE = 180^\circ$
Comparing this equation with $\angle ABC + \angle CBE = 180^\circ$, we get:
$\angle DAB = \angle ABC$
Thus, $\angle A = \angle B$.
Part (i) is proved.
Part (ii): $\angle C = \angle D$
From the linear pair, $\angle ABC + \angle CBE = 180^\circ$. So $\angle B + \angle CBE = 180^\circ$.
From the isosceles triangle $\triangle BCE$, $\angle CBE = \angle CEB$.
From the parallelogram ADCE, opposite angles are equal, so $\angle ADC = \angle AEC$. Note that $\angle AEC$ is the same as $\angle CEB$.
Therefore, $\angle ADC = \angle CEB$.
Since $\angle CBE = \angle CEB$, we have $\angle ADC = \angle CBE$.
$\angle ADC = \angle CBE$
(Both equal to $\angle CEB$)
Substitute this into the linear pair equation $\angle B + \angle CBE = 180^\circ$:
$\angle B + \angle ADC = 180^\circ$
So, $\angle B + \angle D = 180^\circ$.
We know the sum of angles in a quadrilateral is $360^\circ$.
$\angle A + \angle B + \angle C + \angle D = 360^\circ$
Substitute $\angle A = \angle B$ (from Part (i)):
$\angle B + \angle B + \angle C + \angle D = 360^\circ$
$2\angle B + \angle C + \angle D = 360^\circ$
Substitute $\angle B = 180^\circ - \angle D$ (from $\angle B + \angle D = 180^\circ$):
$2(180^\circ - \angle D) + \angle C + \angle D = 360^\circ$
$360^\circ - 2\angle D + \angle C + \angle D = 360^\circ$
$360^\circ - \angle D + \angle C = 360^\circ$
Subtract $360^\circ$ from both sides:
$\angle C - \angle D = 0^\circ$
$\angle C = \angle D$
Thus, $\angle C = \angle D$.
Part (ii) is proved.
Part (iii): $\triangle ABC \cong \triangle BAD$
Consider $\triangle ABC$ and $\triangle BAD$.
AB = BA
(Common side)
BC = AD
(Given)
$\angle ABC = \angle BAD$
(Proven in Part (i), $\angle B = \angle A$)
Therefore, by SAS (Side-Angle-Side) congruence rule,
$\triangle ABC \cong \triangle BAD$
Part (iii) is proved.
Part (iv): diagonal AC = diagonal BD
Since $\triangle ABC \cong \triangle BAD$ (Proven in Part (iii)), the corresponding parts are equal by CPCT (Corresponding Parts of Congruent Triangles are Congruent).
AC = BD
Thus, the diagonals of the trapezium are equal.
Part (iv) is proved.
Example 6 & 7 (Before Exercise 8.2)
Example 6. In ∆ ABC, D, E and F are respectively the mid-points of sides AB, BC and CA (see Fig. 8.18). Show that ∆ ABC is divided into four congruent triangles by joining D, E and F.
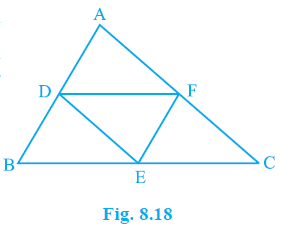
Answer:
Given:
D, E, and F are the mid-points of sides AB, BC, and CA respectively of $\triangle ABC$.
To Prove:
$\triangle ADF \cong \triangle BDE \cong \triangle CEF \cong \triangle DFE$
Proof:
Since D, E, and F are the mid-points of AB, BC, and CA respectively, we can apply the Mid-point Theorem.
By the Mid-point Theorem:
1. The line segment joining the mid-points of two sides of a triangle is parallel to the third side and is half of the third side.
Applying this to $\triangle ABC$:
Joining mid-points D and E of AB and BC respectively:
DE || AC and $DE = \frac{1}{2}AC$
Joining mid-points E and F of BC and CA respectively:
EF || AB and $EF = \frac{1}{2}AB$
Joining mid-points D and F of AB and CA respectively:
DF || BC and $DF = \frac{1}{2}BC$
Also, by the definition of mid-points:
$AD = DB = \frac{1}{2}AB$
$BE = EC = \frac{1}{2}BC$
$AF = FC = \frac{1}{2}AC$
Now let's compare the side lengths of the four small triangles formed: $\triangle ADF$, $\triangle BDE$, $\triangle CEF$, and $\triangle DFE$.
Consider $\triangle ADF$:
AD $= \frac{1}{2}AB$ (Since D is the mid-point)
AF $= \frac{1}{2}AC$ (Since F is the mid-point)
DF $= \frac{1}{2}BC$ (By Mid-point theorem applied to D and F)
Consider $\triangle BDE$:
BD $= \frac{1}{2}AB$ (Since D is the mid-point)
BE $= \frac{1}{2}BC$ (Since E is the mid-point)
DE $= \frac{1}{2}AC$ (By Mid-point theorem applied to D and E)
Consider $\triangle CEF$:
CE $= \frac{1}{2}BC$ (Since E is the mid-point)
CF $= \frac{1}{2}AC$ (Since F is the mid-point)
EF $= \frac{1}{2}AB$ (By Mid-point theorem applied to E and F)
Consider $\triangle DFE$:
DF $= \frac{1}{2}BC$ (By Mid-point theorem applied to D and F)
FE $= \frac{1}{2}AB$ (By Mid-point theorem applied to E and F)
ED $= \frac{1}{2}AC$ (By Mid-point theorem applied to D and E)
Now, let's compare the sides of the four triangles:
Sides of $\triangle ADF$: AD ($=\frac{1}{2}AB$), AF ($=\frac{1}{2}AC$), DF ($=\frac{1}{2}BC$).
Sides of $\triangle BDE$: BD ($=\frac{1}{2}AB$), BE ($=\frac{1}{2}BC$), DE ($=\frac{1}{2}AC$).
Sides of $\triangle CEF$: CE ($=\frac{1}{2}BC$), CF ($=\frac{1}{2}AC$), EF ($=\frac{1}{2}AB$).
Sides of $\triangle DFE$: DF ($=\frac{1}{2}BC$), FE ($=\frac{1}{2}AB$), ED ($=\frac{1}{2}AC$).
All four triangles have sides equal to half the length of the corresponding sides of $\triangle ABC$.
Therefore, by the SSS (Side-Side-Side) congruence rule, all four triangles are congruent to each other.
$\triangle ADF \cong \triangle BDE \cong \triangle CEF \cong \triangle DFE$
Hence, $\triangle ABC$ is divided into four congruent triangles by joining the mid-points D, E, and F.
Example 7. l, m and n are three parallel lines intersected by transversals p and q such that l, m and n cut off equal intercepts AB and BC on p (see Fig. 8.19). Show that l, m and n cut off equal intercepts DE and EF on q also.
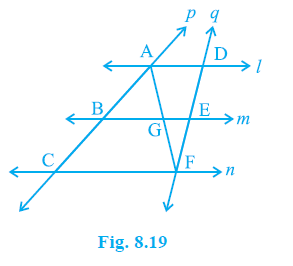
Answer:
Given:
Lines l, m, and n are parallel (l || m || n).
Transversal p intersects lines l, m, and n at points A, B, and C respectively.
Transversal q intersects lines l, m, and n at points D, E, and F respectively.
The intercepts on p are equal, i.e., AB = BC.
To Prove:
The intercepts on q are equal, i.e., DE = EF.
Construction:
Draw a line through point A parallel to transversal q, intersecting line m at point G and line n at point H.
Proof:
Consider the quadrilateral AGED. By construction, AG || q. Since DE is a segment of transversal q, AG || DE.
Lines l and m are parallel (l || m), and A is on l while G and E are on m. So, AD || GE.
Thus, quadrilateral AGED has both pairs of opposite sides parallel, which means it is a parallelogram.
In a parallelogram, opposite sides are equal.
AG = DE
(Opposite sides of parallelogram AGED)
Now consider the figure formed by the parallel lines m, n and the segments GB, KC (where K is on line n such that BK || q). Let's use a second construction line for clarity in the congruence part.
Draw a line through point B parallel to transversal q, intersecting line n at point K.
Consider the quadrilateral BKFE. By construction, BK || q. Since EF is a segment of transversal q, BK || EF.
Lines m and n are parallel (m || n), and B is on m while K and F are on n. So, BE || KF.
Thus, quadrilateral BKFE is a parallelogram.
In a parallelogram, opposite sides are equal.
BK = EF
(Opposite sides of parallelogram BKFE)
Now, consider $\triangle ABG$ and $\triangle BCK$.
We are given that the intercepts on transversal p are equal.
AB = BC
(Given)
Lines AG and BK are both parallel to transversal q (by construction), so AG || BK.
Transversal p intersects the parallel lines AG and BK at points A and B respectively. Therefore, the corresponding angles are equal.
$\angle BAG = \angle CBK$
(Corresponding angles, AG || BK, transversal p)
Lines m and n are parallel (m || n). Line AG is parallel to line BK (AG || BK).
$\angle AGB$ is the angle formed by the intersection of line m and line AG.
$\angle BKC$ is the angle formed by the intersection of line n and line BK.
Since line m is parallel to line n, and line AG is parallel to line BK, the angle between line m and line AG is equal to the angle between line n and line BK.
$\angle AGB = \angle BKC$
(Angles between parallel lines m || n and parallel lines AG || BK)
Now, in $\triangle ABG$ and $\triangle BCK$:
$\angle BAG = \angle CBK$
(Proven above)
$\angle AGB = \angle BKC$
(Proven above)
AB = BC
(Given, non-included side opposite $\angle AGB$ and $\angle BKC$ respectively)
Therefore, by the AAS (Angle-Angle-Side) congruence rule,
$\triangle ABG \cong \triangle BCK$
By CPCT (Corresponding Parts of Congruent Triangles are Congruent), the corresponding sides are equal.
AG = BK
From the parallelogram properties proven earlier, we have:
AG = DE
BK = EF
Substituting AG = BK into these equations, we get DE = EF.
Hence, the parallel lines l, m, and n cut off equal intercepts DE and EF on transversal q.
Exercise 8.2
Question 1. ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see Fig 8.20). AC is a diagonal. Show that :
(i) SR || AC and SR = $\frac{1}{2}$ AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
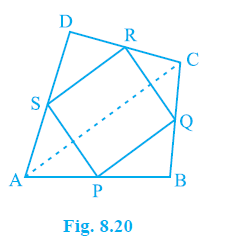
Answer:
Given:
ABCD is a quadrilateral.
P, Q, R, and S are the mid-points of the sides AB, BC, CD, and DA respectively.
AC is a diagonal of the quadrilateral ABCD.
To Prove:
(i) SR || AC and $SR = \frac{1}{2}$ AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
Proof:
Part (i): SR || AC and $SR = \frac{1}{2} AC$
Consider the triangle $\Delta$ ADC.
S is the mid-point of side AD (Given).
R is the mid-point of side CD (Given).
By the Mid-point Theorem, the line segment joining the mid-points of two sides of a triangle is parallel to the third side and is half of the third side.
Applying the Mid-point Theorem to $\Delta$ ADC for the segment SR, we get:
SR || AC (By Mid-point Theorem in $\Delta$ ADC)
SR = $\frac{1}{2}$ AC
... (1)
Thus, we have shown that SR || AC and $SR = \frac{1}{2} AC$.
Part (i) is proved.
Part (ii): PQ = SR
Consider the triangle $\Delta$ ABC.
P is the mid-point of side AB (Given).
Q is the mid-point of side BC (Given).
By the Mid-point Theorem, the line segment joining the mid-points of two sides of a triangle is parallel to the third side and is half of the third side.
Applying the Mid-point Theorem to $\Delta$ ABC for the segment PQ, we get:
PQ || AC (By Mid-point Theorem in $\Delta$ ABC)
PQ = $\frac{1}{2}$ AC
... (2)
Now, compare equation (1) and equation (2).
SR = $\frac{1}{2}$ AC
(From 1)
PQ = $\frac{1}{2}$ AC
(From 2)
Since both SR and PQ are equal to half the length of AC, they must be equal to each other.
PQ = SR
... (3)
Therefore, PQ = SR.
Part (ii) is proved.
Part (iii): PQRS is a parallelogram.
From the Mid-point Theorem applied in $\Delta$ ABC, we know that PQ || AC (as shown in the steps for Part ii).
From the Mid-point Theorem applied in $\Delta$ ADC, we know that SR || AC (as shown in the steps for Part i).
Since both line segments PQ and SR are parallel to the same line segment AC, they must be parallel to each other.
PQ || SR (Lines parallel to the same line are parallel to each other)
From Part (ii), we have already shown that PQ = SR.
PQ = SR
(From 3)
In quadrilateral PQRS, we have shown that one pair of opposite sides (PQ and SR) is both equal and parallel.
A quadrilateral with one pair of opposite sides equal and parallel is a parallelogram.
Therefore, PQRS is a parallelogram.
Part (iii) is proved.
Hence Proved.
Question 2. ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
Answer:
Given:
ABCD is a rhombus.
P, Q, R, and S are the mid-points of sides AB, BC, CD, and DA respectively.
To Prove:
The quadrilateral PQRS is a rectangle.
Figure:
Draw a rhombus ABCD. Mark the midpoints P, Q, R, S on the sides AB, BC, CD, DA respectively. Join the midpoints to form quadrilateral PQRS. Draw the diagonals AC and BD of the rhombus.
Proof:
First, we show that PQRS is a parallelogram using the Mid-point Theorem.
Consider $\Delta$ ABC.
P is the mid-point of AB (Given).
Q is the mid-point of BC (Given).
By the Mid-point Theorem, the line segment joining the mid-points of two sides of a triangle is parallel to the third side and is half of the third side.
Applying the Mid-point Theorem to $\Delta$ ABC for the segment PQ:
PQ || AC
(By Mid-point Theorem in $\Delta$ ABC)
PQ = $\frac{1}{2}$ AC
... (1)
Consider $\Delta$ ADC.
S is the mid-point of AD (Given).
R is the mid-point of CD (Given).
By the Mid-point Theorem in $\Delta$ ADC for the segment SR:
SR || AC
(By Mid-point Theorem in $\Delta$ ADC)
SR = $\frac{1}{2}$ AC
... (2)
From equation (1) and equation (2), we have PQ || AC and SR || AC. Since both are parallel to the same line AC, they are parallel to each other:
PQ || SR
(Lines parallel to the same line are parallel)
Also, from equation (1) and equation (2), $PQ = \frac{1}{2} AC$ and $SR = \frac{1}{2} AC$. Thus, PQ = SR.
PQ = SR
... (3)
Since one pair of opposite sides (PQ and SR) in quadrilateral PQRS is both equal and parallel, PQRS is a parallelogram.
Now, to show that PQRS is a rectangle, we need to prove that one of its interior angles is $90^\circ$.
Consider $\Delta$ ABD.
P is the mid-point of AB (Given).
S is the mid-point of AD (Given).
By the Mid-point Theorem in $\Delta$ ABD for the segment PS:
PS || BD
(By Mid-point Theorem in $\Delta$ ABD)
PS = $\frac{1}{2}$ BD
... (4)
We know a key property of a rhombus: the diagonals of a rhombus bisect each other at right angles.
So, the diagonal AC is perpendicular to the diagonal BD.
AC $\perp$ BD
(Diagonals of a rhombus are perpendicular)
Let the intersection point of AC and BD be O. Then $\angle$ AOB = $90^\circ$.
We have shown that PQ || AC and PS || BD.
Consider the intersection of PQ and PS. Let the line containing PQ be denoted by line $p_{PQ}$ and the line containing PS be denoted by line $l_{PS}$.
Line $p_{PQ}$ is parallel to line AC.
Line $l_{PS}$ is parallel to line BD.
Since line AC is perpendicular to line BD, their parallel lines $p_{PQ}$ and $l_{PS}$ must also be perpendicular to each other.
The angle between $p_{PQ}$ and $l_{PS}$ is the angle $\angle$ SPQ of the quadrilateral PQRS.
$\angle$ SPQ = $90^\circ$
(Angle between lines parallel to perpendicular lines)
We have shown that PQRS is a parallelogram and one of its interior angles ($\angle$ SPQ) is $90^\circ$.
A parallelogram with one right angle is a rectangle.
Thus, PQRS is a rectangle.
Hence Proved.
Question 3. ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
Answer:
Given:
ABCD is a rectangle.
P, Q, R, and S are the mid-points of sides AB, BC, CD, and DA respectively.
To Prove:
The quadrilateral PQRS is a rhombus.
Figure:
Draw a rectangle ABCD. Mark the midpoints P, Q, R, S on the sides AB, BC, CD, DA respectively. Join the midpoints to form quadrilateral PQRS. Draw the diagonals AC and BD of the rectangle.
Proof:
Consider $\Delta$ ABC.
P is the mid-point of AB (Given).
Q is the mid-point of BC (Given).
By the Mid-point Theorem, the line segment joining the mid-points of two sides of a triangle is parallel to the third side and is half of the third side.
Applying the Mid-point Theorem to $\Delta$ ABC for the segment PQ:
PQ || AC
(By Mid-point Theorem in $\Delta$ ABC)
PQ = $\frac{1}{2}$ AC
... (1)
Consider $\Delta$ ADC.
S is the mid-point of AD (Given).
R is the mid-point of CD (Given).
By the Mid-point Theorem in $\Delta$ ADC for the segment SR:
SR || AC
(By Mid-point Theorem in $\Delta$ ADC)
SR = $\frac{1}{2}$ AC
... (2)
From equation (1) and equation (2), we have PQ || AC and SR || AC. Thus, PQ || SR. Also $PQ = \frac{1}{2} AC$ and $SR = \frac{1}{2} AC$, so PQ = SR.
Consider $\Delta$ ABD.
P is the mid-point of AB (Given).
S is the mid-point of AD (Given).
By the Mid-point Theorem in $\Delta$ ABD for the segment PS:
PS || BD
(By Mid-point Theorem in $\Delta$ ABD)
PS = $\frac{1}{2}$ BD
... (3)
Consider $\Delta$ BCD.
Q is the mid-point of BC (Given).
R is the mid-point of CD (Given).
By the Mid-point Theorem in $\Delta$ BCD for the segment QR:
QR || BD
(By Mid-point Theorem in $\Delta$ BCD)
QR = $\frac{1}{2}$ BD
... (4)
We know that the diagonals of a rectangle are equal in length.
AC = BD
(Diagonals of a rectangle are equal)
From equations (1), (2), (3), and (4), and since AC = BD, we can compare the lengths of the sides of PQRS:
PQ = $\frac{1}{2}$ AC
(From 1)
SR = $\frac{1}{2}$ AC
(From 2)
PS = $\frac{1}{2}$ BD
(From 3)
QR = $\frac{1}{2}$ BD
(From 4)
Since AC = BD, it follows that $\frac{1}{2} AC = \frac{1}{2} BD$.
Therefore, $PQ = SR = PS = QR$.
PQ = QR = RS = SP
... (5)
We have shown that all four sides of quadrilateral PQRS are equal (from equation (5)).
We could also prove that PQRS is a parallelogram using the Midpoint Theorem (PQ || AC || SR, so PQ || SR; PS || BD || QR, so PS || QR).
A quadrilateral with all sides equal is a rhombus. Alternatively, a parallelogram with all sides equal is a rhombus.
Thus, the quadrilateral PQRS is a rhombus.
Hence Proved.
Question 4. ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see Fig. 8.21). Show that F is the mid-point of BC.
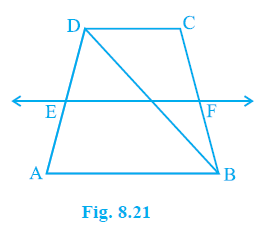
Answer:
Given:
ABCD is a trapezium with AB || DC.
BD is a diagonal.
E is the mid-point of side AD.
A line segment EF is drawn through E such that EF || AB, and EF intersects BC at F.
Since AB || DC (given) and AB || EF (given), it follows that EF || DC (Lines parallel to the same line are parallel to each other).
EF || DC
(Since AB || DC and AB || EF)
To Prove:
F is the mid-point of BC.
Proof:
Let the line segment EF intersect the diagonal BD at point G.
Consider the triangle $\Delta$ ABD.
We are given that E is the mid-point of side AD.
E is mid-point of AD
(Given)
The line segment EG is part of the line EF.
We are given that EF || AB. Since G lies on EF, the segment EG is also parallel to AB.
EG || AB
(Since EF || AB and G is on EF)
In a triangle, a line segment drawn through the mid-point of one side parallel to another side bisects the third side. This is the Converse of the Mid-point Theorem.
Applying the Converse of the Mid-point Theorem to $\Delta$ ABD:
Since E is the mid-point of AD and EG || AB, the line segment EG must bisect the side BD.
Therefore, G is the mid-point of BD.
G is mid-point of BD
(By Converse of Mid-point Theorem in $\Delta$ ABD) ... (1)
Now, consider the triangle $\Delta$ BCD.
From equation (1), we know that G is the mid-point of the diagonal BD.
G is mid-point of BD
(Proven above)
The line segment GF is part of the line EF.
We have established that EF || DC. Since G lies on EF and F lies on EF, the segment GF is also parallel to DC.
GF || DC
(Since EF || DC and G and F are on EF)
Applying the Converse of the Mid-point Theorem to $\Delta$ BCD:
Since G is the mid-point of BD and GF || DC, the line segment GF must bisect the side BC.
Therefore, F is the mid-point of BC.
F is mid-point of BC
(By Converse of Mid-point Theorem in $\Delta$ BCD)
Hence, it is shown that F is the mid-point of BC.
Hence Proved.
Question 5. In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see Fig. 8.22). Show that the line segments AF and EC trisect the diagonal BD.

Answer:
Given:
ABCD is a parallelogram.
E is the mid-point of side AB, and F is the mid-point of side CD.
To Prove:
The line segments AF and EC trisect the diagonal BD.
Let AF intersect the diagonal BD at point P.
Let EC intersect the diagonal BD at point Q.
To prove that AF and EC trisect BD, we need to show that the diagonal BD is divided into three equal parts by points P and Q. That is, we need to prove that DP = PQ = QB.
Proof:
Since ABCD is a parallelogram, its opposite sides are parallel and equal.
AB || DC
(Opposite sides of parallelogram)
AB = DC
(Opposite sides of parallelogram)
E is the mid-point of AB, so $AE = \frac{1}{2}AB$.
F is the mid-point of CD, so $CF = \frac{1}{2}CD$.
Since AB = DC, multiplying by $\frac{1}{2}$ gives $\frac{1}{2}AB = \frac{1}{2}CD$.
AE = CF
... (1)
Also, since AB || DC, the segment AE is parallel to the segment FC (as E lies on AB and F lies on DC).
AE || FC
(Since E is on AB, F is on DC, and AB || DC)
Consider the quadrilateral AECF. From equation (1), we have AE = CF, and we have shown that AE || FC. A quadrilateral with one pair of opposite sides equal and parallel is a parallelogram.
Therefore, AECF is a parallelogram.
Since AECF is a parallelogram, its opposite sides are parallel.
AF || EC
(Opposite sides of parallelogram AECF)
Now, let's consider $\Delta$ ABP.
E is the mid-point of side AB (Given).
E is mid-point of AB
(Given)
The line segment EQ is part of the line segment EC.
We have shown that AF || EC. Since P lies on AF, the line segment AP is parallel to the line segment EC.
Since Q lies on EC, it means the segment EQ is parallel to AP.
EQ || AP
(Since EC || AF, and Q is on EC, P is on AF)
In $\Delta$ ABP, E is the mid-point of AB and EQ is a line segment drawn from E parallel to AP (the other side of the triangle).
By the Converse of the Mid-point Theorem, if a line drawn through the mid-point of one side of a triangle is parallel to another side, then it bisects the third side.
Applying the Converse of the Mid-point Theorem to $\Delta$ ABP with line segment EQ:
Since E is the mid-point of AB and EQ || AP, the line segment EQ must bisect the side BP.
Therefore, Q is the mid-point of BP.
BQ = QP
... (2)
Next, let's consider $\Delta$ CDQ.
F is the mid-point of side CD (Given).
F is mid-point of CD
(Given)
The line segment FP is part of the line segment AF.
We have shown that AF || EC. Since Q lies on EC, the line segment CQ is parallel to the line segment AF.
Since P lies on AF, it means the segment FP is parallel to CQ.
FP || CQ
(Since AF || EC, and P is on AF, Q is on EC)
In $\Delta$ CDQ, F is the mid-point of CD and FP is a line segment drawn from F parallel to CQ (the other side of the triangle).
Applying the Converse of the Mid-point Theorem to $\Delta$ CDQ with line segment FP:
Since F is the mid-point of CD and FP || CQ, the line segment FP must bisect the side DQ.
Therefore, P is the mid-point of DQ.
DP = PQ
... (3)
From equation (2), we have BQ = PQ.
From equation (3), we have DP = PQ.
Combining these two results, we get:
DP = PQ = BQ
... (4)
This shows that the diagonal BD is divided into three equal parts (DP, PQ, and QB) by the intersection points P and Q of the line segments AF and EC.
Hence, the line segments AF and EC trisect the diagonal BD.
Hence Proved.
Question 6. ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) MD ⊥ AC
(iii) CM = MA = $\frac{1}{2}$ AB
Answer:
Given:
In $\Delta$ ABC, $\angle$ C = $90^\circ$.
M is the mid-point of the hypotenuse AB.
A line is drawn through M such that this line is parallel to BC and intersects AC at point D.
MD || BC
(Given)
To Prove:
(i) D is the mid-point of AC.
(ii) MD $\perp$ AC.
(iii) CM = MA = $\frac{1}{2}$ AB.
Figure:
Draw a right-angled triangle ABC with the right angle at C. Mark the midpoint M of the hypotenuse AB. Draw a line through M parallel to BC that intersects AC at D. Join C to M.
Proof:
Part (i): D is the mid-point of AC.
Consider $\Delta$ ABC.
M is the mid-point of side AB (Given).
M is mid-point of AB
(Given)
The line segment MD is parallel to side BC (Given).
MD || BC
(Given)
By the Converse of the Mid-point Theorem, if a line is drawn through the mid-point of one side of a triangle parallel to another side, then it bisects the third side.
Applying the Converse of the Mid-point Theorem to $\Delta$ ABC:
Since M is the mid-point of AB and MD || BC, the line segment MD must bisect the side AC.
Therefore, D is the mid-point of AC.
Part (i) is proved.
Part (ii): MD $\perp$ AC.
We are given that MD || BC.
We are given that $\Delta$ ABC is right-angled at C, which means that the sides BC and AC are perpendicular to each other.
BC $\perp$ AC
(Given $\angle$ C = $90^\circ$)
Since MD is parallel to BC and BC is perpendicular to AC, it follows that MD must also be perpendicular to AC.
MD $\perp$ AC
(A line parallel to a perpendicular line is also perpendicular)
This means that the angle formed by MD and AC is $90^\circ$ at point D.
$\angle$ MDA = $90^\circ$
Part (ii) is proved.
Part (iii): CM = MA = $\frac{1}{2}$ AB.
Since M is the mid-point of the hypotenuse AB (given), we know that MA is half the length of AB.
MA = $\frac{1}{2}$ AB
(M is mid-point of AB) ... (1)
Now consider the triangles $\Delta$ AMD and $\Delta$ CMD.
1. Side AD and side CD are equal.
AD = CD
(D is the mid-point of AC, proven in Part (i))
2. The angles $\angle$ MDA and $\angle$ MDC are right angles.
$\angle$ MDA = $\angle$ MDC
(Both equal to $90^\circ$, proven in Part (ii))
3. Side MD is common to both triangles.
MD = MD
(Common side)
Therefore, by the SAS (Side-Angle-Side) congruence rule, $\Delta$ AMD is congruent to $\Delta$ CMD.
$\Delta$ AMD $\cong$ $\Delta$ CMD
... (2)
By CPCT (Corresponding Parts of Congruent Triangles), the corresponding sides are equal.
The side CM in $\Delta$ CMD corresponds to the side MA in $\Delta$ AMD.
CM = MA
(By CPCT) ... (3)
Combining the results from equation (1) ($MA = \frac{1}{2} AB$) and equation (3) (CM = MA), we get:
CM = MA = $\frac{1}{2}$ AB
Part (iii) is proved.
Hence Proved.

